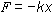
By measuring the size of an indentation made by a measured force, it is possible to estimate the hardness of the sample surface. This is analogous to industrial hardness tests (e.g., Rockwell and Brinell tests) however, at the nanometric level precise one-to-one comparisons are elusive.
To calculate the force applied to the sample during indentation it is necessary to first measure the cantilever sensitivity. The cantilever sensitivity, called the Deflection sens. or TM Deflection Sens. in the software, is the cantilever deflection signal versus the voltage applied to the Z piezo determined from the slope of the force plot during indentation. The cantilever sensitivity is a conversion factor from cantilever deflection in volts to cantilever deflection in nm. Its units are nm/volt. Once the sensitivity is known, the force (F) of indentation is determined from Hooke's Law:
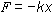
where k is the spring constant in N/m and x is the cantilever deflection (for this particular case). The cantilever deflection is determined from the cantilever sensitivity and the maximum deflection used for the indentation (Trigger threshold).
in N/m and x is the cantilever deflection (for this particular case). The cantilever deflection is determined from the cantilever sensitivity and the maximum deflection used for the indentation (Trigger threshold).
It is more accurate to measure the cantilever sensitivity on a very hard sample, since there is little surface penetration. Since the cantilever sensitivity is a measurement of the change in cantilever deflection per change in the Z position, it is important to have negligible sample penetration. If a change in Z position causes not only cantilever deflection but also sample penetration, the sensitivity measurement is inaccurate. For a soft sample, more Z motion is required to obtain the same deflection as on a hard sample. Thus the sensitivity is greater when measured on a harder sample.
The ideal sensitivity would be obtained on an infinitely hard sample. The ideal sensitivity is approached as the sample penetration approaches zero or as the hardness becomes infinite. It is suggested that a hard sample, such as the sapphire sample provided with the nanoindentation package, is used to measure the cantilever sensitivity before or after indenting the desired sample. The more accurate you need your calculation of the indentation force to be, the more important this becomes.
The procedures for Force Calibration vary according to the mode selected. For detailed force calibration information, including procedures, see:
Nanoindentation is best suited for making relative, rather than absolute, hardness measurements. When making hardness comparisons, it is imperative that conditions be replicated as best as possible, preferably using the same diamond tip without repositioning the tip or changing the position of the laser spot on the cantilever during the tests. If it is necessary to compare many samples or many locations within a sample, or if the tip is replaced, note the following:
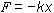
Force (N) = Spring constant (N/m) x Trigger threshold (V) x Sensitivity (nm/V) x units conversion factor
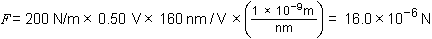
Here, k (200 N/m) is multiplied by the Trigger threshold times the Deflection sensitivity. The conversion factor, (1 x 10-–9 m /1 nm) is multiplied to convert the units properly to Newtons. It is absolutely critical that the cantilever’s sensitivity be calibrated as part of the force-measuring procedure; otherwise, results will be wrong.
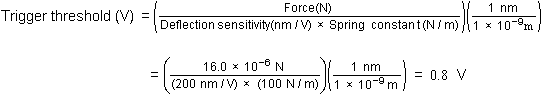
That is, by setting the Trigger threshold of tip “B” to 0.8 V, the same amount of force should be delivered to the surface as when using tip “A.” By observing dents creating by the two tips on the same sample surface, it is possible to obtain a subjective comparison. For this reason, it is useful to keep a “touchstone” nanoindentation standard. Recall that indentation sizes vary depending upon the sharpness of the diamond, even for tips mounted on cantilevers having the same spring constant. If the observed dents are grossly different, recheck the calculations—the Trigger threshold may be set incorrectly.
| www.bruker.com | Bruker Corporation |
| www.brukerafmprobes.com | 112 Robin Hill Rd. |
| nanoscaleworld.bruker-axs.com/nanoscaleworld/ | Santa Barbara, CA 93117 |
| Customer Support: (800) 873-9750 | |
| Copyright 2010, 2011. All Rights Reserved. |