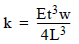
This method of Spring Constant Calibration contrasts with Estimation from Cantilever Geometry in that it requires careful work but yields a more accurate value. The user must measure the resonant frequency before and after adding a known mass to the cantilever. The shift in resonant frequency is used to derive the cantilever spring constant.
The method is described here for a model appropriate to TappingMode probes: a single-beam cantilever of rectangular cross-section, whose spring constant is given by Equation 1:
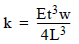
where:
E = elastic modulus (Young’s Modulus)
t = cantilever thickness
w = cantilever width
L = cantilever length
The resonant frequency of such a beam is given by Equation 2:
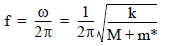
where:
m* = the effective mass (>> 0.24m, for beam mass m = ρtwL; ρ = the cantilever density)
M = the known mass added to the cantilever's free end
Re-arranging the last equation, added mass, M, varies linearly with (2pf)–2. That is, M = k(2pf)–2 –m*. As a linear relation, comparing the resonant frequency with added mass to that without is sufficient to solve for both the spring constant and the effective mass of the cantilever:
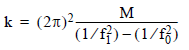
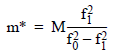
The first solution of the simultaneous equations provides the spring constant, given the added mass and the two resonant frequencies, with added mass (f1) and without (f0). The accuracy of the spring constant determination depends primarily on the uncertainty in the added mass, as the resonant frequencies typically may be measured to higher precision.
Various methods have been used to affix particles to cantilevers. Three such procedures, developed by researchers using Bruker systems, are detailed in Support Note 226B, Attaching Particles to AFM Cantilevers. By using a cantilever before calibrating it, one can avoid the step of removing the added mass to perform an experiment with a calibrated cantilever.
Substituting Equation 1 (the expression for spring constant in terms of cantilever geometry and material properties, k[E,t,w,L]), into Equation 2 (the expression for cantilever resonant frequency in terms of spring constant and mass components, f[k,M,m*]), results in an equation, f(E,t,w,L,M,m*), which expresses cantilever resonant frequency in terms of geometric characteristics. Rearranging the new equation as an expression of cantilever thickness in terms of the other variables, now including resonant frequency, that is, as t(E,w,L,M,m*,f), then substituting this rearranged equation for thickness back into the first equation demonstrates that spring constant is proportional to resonant frequency cubed, independent of cantilever thickness:
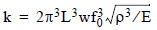
For further discussion of this derivation, refer to A Nondestructive Method for Determining the Spring Constant of Cantilevers for Scanning Force Microscopy, by J. P. Cleveland, et. al., in Review of Scientific Instruments, 64 (2), February 1993, page 403.
| www.bruker.com | Bruker Corporation |
| www.brukerafmprobes.com | 112 Robin Hill Rd. |
| nanoscaleworld.bruker-axs.com/nanoscaleworld/ | Santa Barbara, CA 93117 |
| Customer Support: (800) 873-9750 | |
| Copyright 2010, 2011. All Rights Reserved. |