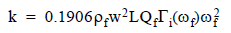
By comparing resonance in vacuum to resonance in fluid for a rectangular cantilever and introducing the hydrodynamic function, Γ(ω), which depends on the fluid Reynolds number, the cantilever spring constant is computed from easily obtained resonance characteristics and the less variable of probe dimensions:
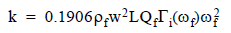
where:
w = cantilever width
L = cantilever length
ρf = density of the fluid (e.g., 1.18kg/m3 for air)
Qf = cantilever resonance quality factor in fluid
ωf = cantilever resonant frequency in the fluid
Γi, the imaginary component of the hydrodynamic function, Γ(ω), where:
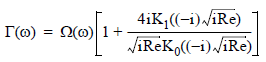
and
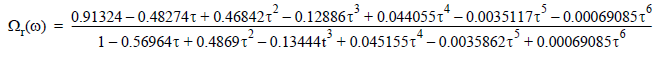
and
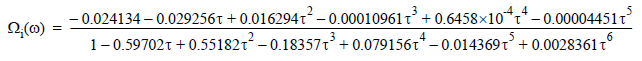
where:
τ = log10(Re)
Reynolds number, Re = ρfωw2/(4η) for fluid viscosity η
K0 and K1 are modified Bessel functions of the third degree (refer to a source for mathematical functions).
The simplicity of data acquisition and computation (once the equations are set up!) are balanced by a few limitations to the method:
For a derivation of this method, refer to Calibration of Rectangular Atomic Force Microscope Cantilevers, John E. Sader, James W. M. Chon and Paul Mulvaney, Review of Scientific Instruments, Vol. 70 (10), October 1999.
| www.bruker.com | Bruker Corporation |
| www.brukerafmprobes.com | 112 Robin Hill Rd. |
| nanoscaleworld.bruker-axs.com/nanoscaleworld/ | Santa Barbara, CA 93117 |
| Customer Support: (800) 873-9750 | |
| Copyright 2010, 2011. All Rights Reserved. |